Solving Systems of Linear Inequalities

Example

Graph the system of inequalities.

y
y + 2	> x

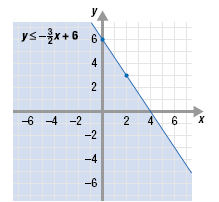
Solution

Step 1 Solve the first inequality for y. Then graph the inequality.

To graph the inequality first graph the equation

• The y-intercept is (0, 6). Plot (0, 6).

• The slope is To find a second point on the line, start at (0, 6) and move down 3 and right 2 to the point (2, 3). Plot (2, 3).

For the inequality the inequality symbol is “≤”. This stands for “is less than or equal to.”

• To represent “equal to,” draw a solid line through (0, 6) and (2, 3).

• To represent “less than,” shade the region below the line.

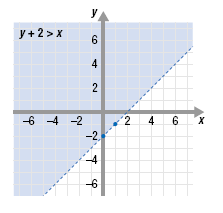
Note:

If you use the slope to plot several more points, it will be easier to draw the line.

Step 2 Solve the second inequality for y. Then graph the inequality.

To solve for y, subtract 2 from both sides of y + 2 > x.

The result is y > x - 2.

To graph y > x - 2, first graph the equation y = x - 2.

• The y-intercept is (0, -2). Plot (0, -2).

• The slope is To find a second point on the line, start at (0, -2) and move up 1 and right 1 to the point (1, -1). Plot (1, -1).

For the inequality y > x - 2, the inequality symbol is “>”. This stands for “is greater than.”

• Since the inequality symbol “>” does not contain “equal to,” draw a dotted line through (0, -2) and (1, -1).

• To represent “greater than,” shade the region above the line.

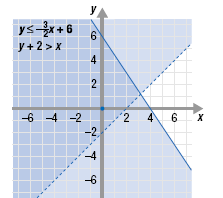
Step 3 Shade the region where the two graphs overlap.

The solution is the region where the graphs overlap. This region contains the points that satisfy both inequalities.

As a check, choose a point in the solution region. For example, choose (0, 0).

To confirm that (0, 0) is a solution of the system, substitute 0 for x and 0 for y in each original inequalities and simplify.

	First inequality			Second inequality
y Is Is	≤ 6 ? Yes		Is Is	y + 2 0 + 2 2	> x > 0 ? > 0 ? Yes

Since (0, 0) satisfies each inequality, it is a solution of the system.

Note:

The solution of the system is the set of all points in the dark shaded region, including the points on the line