Solving Nonlinear Equations by Substitution

Example

Solve for w: w^-2 - 2w^-1 = 15

Solution Step 1 Write the equation in quadratic form. Subtract 15 from both sides. Write w^-2 as (w^-1)². Step 2 Use an appropriate “u” substitution. Substitute u for w^-1. Step 3 Solve the resulting equation. Factor the new equation. Use the Zero Product Property. Solve each equation for u. Step 4 Substitute the original expression for u. Step 5 Solve for the original variable.	w^-2 - 2w^-1 w^-2 - 2w^-1 - 15 (w^-1)² - 2(w^-1)¹ - 15 u² - 2u - 15 (u - 5)(u + 3) u - 5 = 0 or u + 3 u = 5 or u w^-1 = 5 or w^-1	= 15 = 0 = 0 = 0 = 0 = 0 = -3 = -3
Use the definition of a negative exponent.		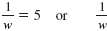= -3
Multiply by the LCD, w.	1 = 5w or 1	= -3w
Divide by the coefficient of w.		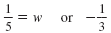= w

So, there are two solutions:

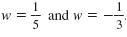
The equation w^-2 - 2w^-1 = 15 written in standard form is w^-2 - 2w^-1 - 15 = 0. The graph of the corresponding function, f(w) = w^-2 - 2w^-1 - 15 is shown.

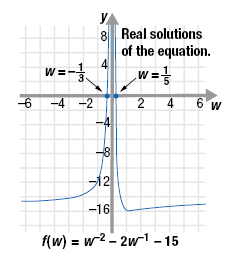
The graph crosses the w-axis at two locations,

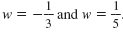
Note that w^-1 can be written as 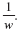Since w is in the denominator it cannot equal 0. Therefore the line w = 0 is a vertical asymptote.