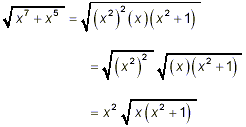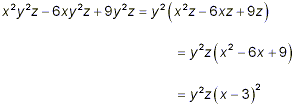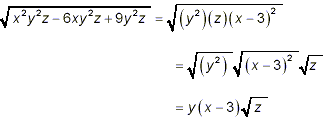Simplifying Square Roots

An expression containing a square root is considered to be as simple as possible when the expression inside the square root is as simple or small as possible. The reduction of the contents inside the square root is accomplished (when possible) by a very straightforward strategy:

(i) Factor the expression inside the square root completely. Write factors which are perfect squares as explicit squares.

(ii) Use the property that the square root of a product is equal to the product of the square roots of the factors to rewrite the square root from step (i) as a product of square roots of factors which are perfect squares and a single square root of an expression which contains no perfect square factors. The pattern is:

where u, v, etc. are perfect squares, and w is an expression containing no perfect square factors. (This may seem a bit abstract, but the meaning of this pattern should become more obvious after you have studied a few of the examples below. It is important in mathematics not only to study specific examples of a type of operation, but to eventually understand an overall general strategy or pattern for similar types of problems.

(iii) Replace the square roots of perfect squares by factors which are not square roots using the property

We now illustrate this general strategy with a series of specific examples.

Example 1:

Simplify

solution:

The method to be used here has been well illustrated already, so you should use this example as a practice problem – try to solve it yourself before looking at the solution that follows.

Since

x ⁷ + x ⁵ = x ⁵ (x ² + 1) = (x ⁴ )(x)(x ² + 1) = (x ² ) ² (x)(x ² + 1)

we can write

as the most simplified form. Probably most practitioners would leave the expression in the radical factored in this way even though this factored form doesn’t help simplify the overall expression any further.

Example 2:

Simplify

solution:

Although this looks like a somewhat more complicated problem than in the previous examples, the same strategy is still applied. First, we factor the expression in the radical as much as possible.

Here, we recognized that after removal of the monomial factors, y ² and z, the remaining expression, x ² – 6x + 9, was a trinomial in x, and so might be factorizable into the form (x + a)(x + b). Using the systematic approach for deducing such factors as we described and illustrated it in an earlier section of these notes, we were able to determine that

x ² – 6x + 9 = (x – 3)(x – 3) = (x – 3) ²

Thus, we can now write

as the final, most simplified, result.