	Algebra Tutorials!



	Home
	Solving Quadratic Equations by Completing the Square
	Graphing Logarithmic Functions
	Division Property of Exponents
	Adding and Subtracting Rational Expressions With Like Denominators
	Rationalizing the Denominator
	Multiplying Special Polynomials
	Functions
	Solving Linear Systems of Equations by Elimination
	Solving Systems of Equation by Substitution and Elimination
	Polynomial Equations
	Solving Linear Systems of Equations by Graphing
	Quadratic Functions
	Solving Proportions
	Parallel and Perpendicular Lines
	Simplifying Square Roots
	Simplifying Fractions
	Adding and Subtracting Fractions
	Adding and Subtracting Fractions
	Solving Linear Equations
	Inequalities in one Variable
	Recognizing Polynomial Equations from their Graphs
	Scientific Notation
	Factoring a Sum or Difference of Two Cubes
	Solving Nonlinear Equations by Substitution
	Solving Systems of Linear Inequalities
	Arithmetics with Decimals
	Finding the Equation of an Inverse Function
	Plotting Points in the Coordinate Plane
	The Product of the Roots of a Quadratic
	Powers
	Solving Quadratic Equations by Completing the Square

Try the Free Math Solver or Scroll down to Tutorials!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

Plotting Points in the Coordinate Plane

Ordered Pairs

An equation in two variables, such as y = 2x + 3, is satisfied only if we find a value for x and a value for y that make it true. For example, if x = 4 and y = 11, then the equation becomes 11 = 2 Â· 4 + 3, which is a true statement. We write x = 4 and y = 11 as the ordered pair (4, 11). The order of the numbers in an ordered pair is important. For example, (5, 13) also satisfies y = 2x + 3 because using 5 for x and 13 for y gives 13 = 2 Â· 5 + 3. However, (13, 5) does not satisfy this equation because 5 ≠ 2 Â· 13 + 3. In an ordered pair the value for x, the x-coordinate, is always written first and the value for y, the y-coordinate, is second: (x, y).

Example 1

Writing ordered pairs

Complete the following ordered pairs so that each ordered pair satisfies the equation 4x + y = 5.

a) (-2, )

b) ( , 3)

Solution

a) Replace x with -2 in 4x + y = 5 because the x-coordinate is -2:

4(-2) + y	= 5
-8 + y	= 5
y	= 13

So the y-coordinate is 13 and the ordered pair is (-2, 13).

b) Replace y with 3 in 4x + y = 5 because the y-coordinate is 3:

4x + 3	= 5
4x	= 2
x

So the x-coordinate is and the ordered pair is .

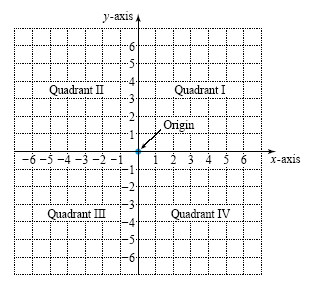
Plotting Points

To graph ordered pairs of real numbers, we need a new coordinate system. The rectangular or Cartesian coordinate system consists of a horizontal number line, the x-axis, and a vertical number line, the y-axis, as shown in the figure below. The intersection of the axes is the origin. The axes divide the coordinate plane, or the xy-plane, into four regions called quadrants. The quadrants are numbered as shown in the figure below, and they do not include any points on the axes.

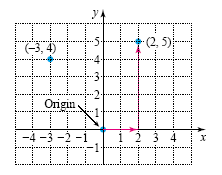
Just as every real number corresponds to a point on the number line, every pair of real numbers corresponds to a point in the rectangular coordinate system. For example, the pair (2, 5) corresponds to the point that lies two units to the right of the origin and five units up. See the figure below. To locate (-3, 4), start at the origin and move three units to the left and four units upward, as in the figure below. Locating a point in the rectangular coordinate system is referred to as plotting or graphing the point.

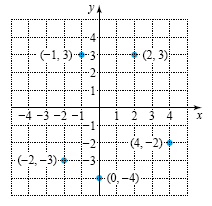
Example 2

Graphing ordered pairs

Plot the points (2, 3), (-2, -3), (-1, 3), (0, -4), and (4, -2).

Solution

To plot (2, 3), start at the origin, move two units to the right, then up three units. To graph (-2, -3), start at the origin, move two units to the left, then down three units. All five points are shown in the figure below.