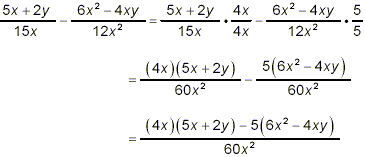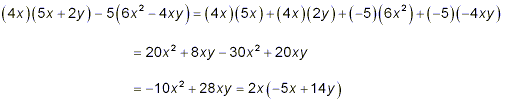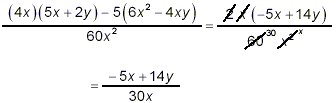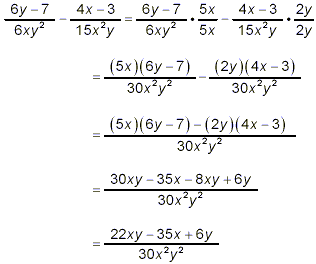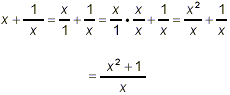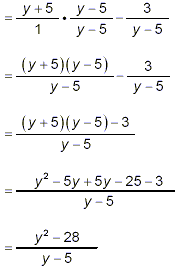Adding and Subtracting Fractions

Addition and subtraction of algebraic fractions works basically the same way as does addition and subtraction of simple numerical fractions:

(i.) rewrite all of the fractions as mathematically equivalent fractions, but having the same denominator (ideally, the simplest such common denominator).

(ii.) combine the numerators of these fractions as indicated (adding and subtracting), retaining the common denominator.

When we work with algebraic fractions, there is then often a third very important step:

(iii.) simplify the resulting fraction as much as possible. It is always necessary to make sure that once the addition/subtraction step is completed, you make a reasonable effort to simplify the result. Usually this simplification step will be made very much easier if you take care in step (i.) to make sure that you have used the simplest possible common denominator. We will illustrate the process for determining that simplest possible denominator when the fractions to be added/subtracted are algebraic fractions. You will see that the strategy is essentially the same as the strategy used to determine the least common denominator when adding or subtracting numerical fractions, except that now symbolic factors may occur as well as numerical factors.

Example 1: Combine and simplify:

solution:

Here, the two denominators share some factors in common and so the simplest common denominator for these fractions is not simply the product of the two denominators. Noting that

15x = (3)(5)(x)

and

12x ² = (2 ²)(3)(x ²)

we conclude that the simplest common denominator here is (2 ²)(3)(5)(x ²) = 60x ². So

The numerator is a difference of two terms, and so we try multiplying to remove the brackets followed by collection of like terms in hope of being able to achieve some simplification.

When the like terms were combined, we noticed that the two terms remaining shared a common factor of 2x, which has been factored out in the last line. Thus, our original difference of two fractions becomes

as the final answer. Since what is left in the numerator cannot be factored further, this is as simple as we can get for the final answer.

Example 2:

Simplify

solution:

As mentioned before, the instruction to “simplify” here means combine the two fractions into a single fraction, and reduce that resulting single fraction to as simple a form as possible. We’ve now done several examples of this type, so here we’ll more or less just show the work without including a lot of discussion. This would be a good example for you to try as a practice exercise before you look at our solution given below.

The two denominators factor as

6xy ² = (2)(3)(x)(y ²)

and

15x ² y = (3)(5)(x ²)(y)

Thus, the simplest common denominator is

(2)(3)(5)(x ²)(y ²) = 30x ² y ²

So, going back to the original problem

There is no obvious way to factor this numerator, so it does not appear that any further simplification of this fraction is possible. So, the last form above must be the requested final answer.

Example 3:

Simplify

solution:

Some people experience an overwhelming temptation here to simply cancel the x’s:

confusing this addition problem with the much simpler multiplication problem

where the cancellation to get the simple result ‘1’ is justified. However, no such quick cancellations can be done in the addition problem we have here because the two x’s aren’t even part of the same fraction! In fact, the first term here is not even a fraction.

Perhaps the clearest way to proceed is to turn the first term into a fraction with denominator equal to 1, and then apply the methods of the previous examples for adding two fractions. We get

This is the final answer, since the numerator cannot be factored further and so there is no additional simplification possible.

Example 4:

Combine and simplify:

solution:

Again, we start by turning this problem into a problem with two fractions, and then we just apply the methods already illustrated in the previous examples.

The simple form of this last fraction is obtained from the previous step by collecting like terms in the numerator. The terms -5y + 5y add up to zero y’s, and the two numbers sum to -28. The numerator of the final fraction shown above, y ² – 28, cannot be factored further to give a form that leads to cancellations with the denominator, so this must be the required final answer.