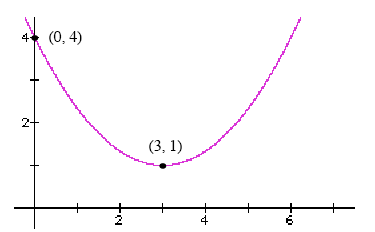
Polynomial Equations

Polynomial Equations in Disguise

The standard format (or standard form) for the formula of a polynomial equation is:

y = c₀ + c₁·x + c₂·x² + ... + c_n·xⁿ

where the powers of x must be positive integers and the letters c₀, c₁, … , c_n represent numbers.

The formulas of polynomial equations sometimes come expressed in other formats, such as factored form or vertex form. The specific format that the formula of a polynomial equation is expressed in does not matter so much – you can always convert the formula to standard form by foiling to check that the formula really is the formula of a polynomial equation.

Example

Figure 2 shows the graph of a quadratic equation.

(a) Find a formula for the quadratic equation expressed in vertex form.

(b) Find a formula for the quadratic equation expressed in standard form.

(c) Is the equation that you have found a formula for a polynomial equation or not?

Figure 1: Find the formula of this quadratic equation.

Solution

(a) The vertex form of a quadratic equation looks like: 

y = a · (x - h)² + k,

where the letter h is the x-coordinate of the vertex and the letter k is the ycoordinate of the vertex. Figure 1 shows that the x-coordinate of the vertex is equal to 3 and that the y-coordinate of the vertex is equal to 1. This means that the vertex form of this quadratic will be: 

y = a · (x - 3)² +1.

All that remains is to find the numerical value of the constant a. To do this, you can use the x- and y-coordinates of any other point (i.e. other than the vertex) that lies on the quadratic – for example the point (0, 4) shown in Figure 2. To work out the value of a we will plug x = 0 and y = 4 into the vertex form and then solve for a. 

4 = a · (0 - 3)² +1. 

4 = a · 9 +1. 

3 = a · 9.

So, the equation for the quadratic equation shown in Figure 1 (expressed in vertex form) is: 

To convert this equation from vertex form to standard form, you can expand by FOILing and then collect like terms. 

(Expand the (x – 3)2 by FOILing)

(Multiply through by one third) 

(Combine the like terms)

So, the equation for the quadratic equation shown in Figure 2 (expressed in standard form) is: 

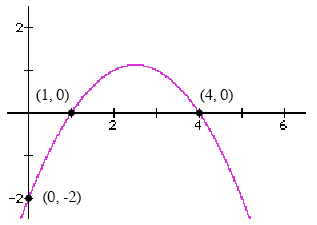
(c) This is a polynomial equation because the formula consists of powers of x added together. All of the powers that appear are positive integers.

Example

Figure2 (see below) shows the graph of a quadratic equation.

(a) Find a formula for the quadratic equation expressed in factored form.

(b) Find a formula for the quadratic equation expressed in standard form.

(c) Is the equation that you have found a formula for a polynomial equation or not?

Figure 2: Find the formula of this quadratic equation.

Solution

(a) The x-intercepts of the quadratic shown in Figure 2 are located at x = 1 and x = 4. This means that the factored form of the quadratic equation must look something like this: 

y = a · (x -1) · (x - 4).

The factored form must have a factor of (x - 1) to ensure that when you plug in x = 1 the value of y will be equal to zero. The factored form must also have a factor of (x - 4) to ensure that when you plug in x = 4 the value of y will be equal to zero.

To determine the numerical value of a you can plug in the x- and y-coordinates of any other point on the quadratic graph (i.e. any point other than one of the xintercepts) and solve for a. Figure 2 shows that the point (0, -2) lies on the graph, so you can plug in x = 0 and y = -2 into the factored form. Doing this: 

-2 = a · (0 -1) · (0 - 4) 

-2 = a · 4 

So, the equation of the quadratic equation from Figure 2 (written in factored form) is:

(b) To convert this equation to standard form, you can expand by FOILing and then simplify (if necessary). Doing this: 

(Expand by FOILing)

(Multiply through by  - beware of “-” signs)

(c) This is a polynomial equation because the formula consists of powers of x added together. All of the powers that appear are positive integers.